원의 비밀, 원주율 π 탐험기
안녕하세요 여러분! 오늘 우리가 탐험할 세계는 바로 원둘레 구하는 공식입니다. 여기에는 무한한 가능성을 품은 신비한 숫자, 원주율 π가 존재합니다. 이 숫자는 단순히 원의 둘레와 지름 사이의 비율을 넘어, 우주의 근본을 탐구하는 열쇠 중 하나랍니다.

원의 둘레를 품은 신비, 원주율 π
원주율 π는 약 3.14159…로 시작하는 끝없는 무한 소수입니다. 이 신비로운 숫자는 원의 둘레를 지름으로 나눈 값으로, 세상의 모든 원에서 일정하게 나타납니다. 바로 이 점이 π의 마법 같은 매력이죠.
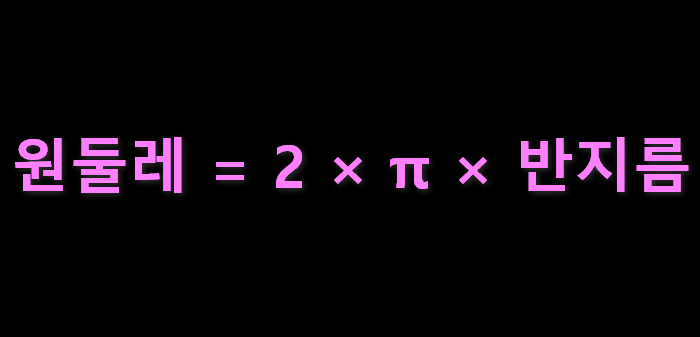
원둘레 구하는 공식 π의 사용방법
원의 둘레를 구하고 싶다면, 이 간단한 공식을 외워보세요.
“원둘레 = 2 × π × 반지름”
반지름이 주어진 원에 이 공식을 적용하면, 마법처럼 그 둘레의 길이를 알아낼 수 있답니다. 예를 들어, 반지름이 7인 원의 둘레는 대략 44를 조금 넘는 수치가 됩니다. 신기하지 않나요?
좀 더 설명하자면 위에서 말한 원둘레에서 원주율은 π로 표기하고, 반지름은 r로 표기합니다. 이 공식은 원의 둘레와 지름의 비율이 항상 일정하다는 원주율의 정의에 기반합니다.
즉, 원의 둘레를 지름으로 나누면 항상 원주율이 나오는 것입니다. 이 공식을 이용하면, 원의 반지름을 알면 원의 둘레를 쉽게 구할 수 있습니다. 예를 들어, 원의 반지름이 10cm라면, 원의 둘레는 다음과 같이 구할 수 있습니다.
원둘레 = 2 × 원주율 × 10cm = 2 × 3.14159265359 × 10cm
따라서, 원의 반지름이 10cm인 경우, 원의 둘레는 약 62.8318530718cm입니다. 이렇게 원둘레를 구하는 공식은 간단하고 쉽게 적용할 수 있습니다.
원주율 π의 역사
원주율 π는 수천 년 전부터 인류의 흥미를 끌어왔어요. 고대 이집트와 바빌로니아에서부터 그리스의 철학자들까지, 많은 사람들이 π의 정확한 값을 찾기 위해 노력했답니다. 그 과정에서 π는 점점 더 정확하게 계산되어 오늘날에는 수조 자리까지 알려져 있어요. 하지만 여전히 π는 그 끝을 알 수 없는 무한의 여정을 이어가고 있죠.
원주율 π의 활용
원주율 π는 단순히 수학 문제를 푸는 데 그치지 않아요. 건축, 공학, 컴퓨터 과학, 물리학 등 다양한 분야에서 중요한 역할을 합니다. 예를 들어, 파이를 사용하여 행성의 궤도를 계산하거나, 다리와 건물의 구조를 설계할 때도 필요해요. 심지어 음악과 예술 속에서도 π의 영향을 찾아볼 수 있답니다.
이제 여러분도 원주율 π의 신비로운 세계로 여행을 떠날 준비가 되셨나요? 원의 둘레를 계산하는 것에서 시작해, 우주의 깊은 비밀까지 탐험할 수 있는 이 여정에서 π는 항상 여러분과 함께할 거예요.