이차방정식 풀이가 복잡할 땐? 근의 공식 계산기 로 쉽게 해결하세요!
안녕하세요. 이번 글은 근의 공식 계산기 에 대한 것 입니다. 저처럼 수학 시간에 이차방정식 문제를 풀다가 머리를 싸매본 경험, 다들 있으시죠? 사실 이차방정식은 수학에서 꽤나 중요한 부분을 차지하고 있어요. 필자도 학교 다닐때 고생 좀 했죠. 아무튼 수많은 공식들 중에서도 근의 공식 은 정말 중요한 공식입니다. 다들 그렇겠지만 이 공식을 이용해서 방정식을 풀 때 가끔 어려움을 느낄 수도 있습니다. 그래서 오늘은 근의 공식 계산기 를 소개해드리려고 해요!
근의 공식 계산기로 직접 계산해보세요!
바로 아래에서 직접 근의 공식을 이용해 방정식을 풀어볼 수 있습니다. 간단히 계수만 입력하면, 빠르고 정확하게 해답을 찾아주는 근의 공식 계산기입니다.
근의 공식 계산기
계산하기
사용법
위 입력란에 이차방정식의 계수 a, b, c를 입력하세요.
'계산하기' 버튼을 클릭하세요.
결과와 상세한 계산 과정이 아래에 표시됩니다.
b가 짝수일 경우, 짝수 버전의 근의 공식도 함께 계산됩니다.
참고: 모든 계수는 실수여야 합니다. a ≠ 0 이어야 합니다.
2. 중근 계산:
`;
steps += `
x = -${b} / (2 × ${a}) = ${x.toFixed(4)}
`;
} else {
result = '
실근이 없습니다. (허근)
';
steps += `
2. 판별식이 음수이므로 실근이 존재하지 않습니다.
`;
}
}
document.getElementById('result').innerHTML = result;
document.getElementById('steps').innerHTML = steps;
}
근의 공식 계산기 사용 방법
이제 여러분이 직접 계산할 차례입니다! 복잡한 계산 과정을 빠르고 쉽게 해결해줄 근의 공식 계산기 를 사용해보세요.
계수 입력: 위의 입력란에 a, b, c 값을 입력합니다. 이 값들은 방정식의 계수입니다.계산 버튼 클릭: 입력이 끝났다면 “계산” 버튼을 클릭하세요!결과 확인: 계산된 결과와 풀이 과정이 하단에 바로 표시됩니다. 각 단계가 어떻게 이루어졌는지 설명까지 함께 확인할 수 있어요.
이 계산기는 단순히 결과만 보여주는 게 아니라, 계산 과정도 하나하나 자세히 설명 해줍니다. 그래서 수학을 공부하는 학생들에게도, 방정식을 풀고 싶은 사람들에게도 큰 도움이 될 거예요.
짝수 버전도 지원합니다!
혹시 b가 짝수일 때, 조금 더 간단한 방식으로 풀고 싶으신가요? 그렇다면 근의 공식의 짝수 버전도 한번 사용해보세요. 우리 계산기에서는 이 방법도 지원합니다! b가 짝수일 때는 계산이 조금 더 간단해질 수 있답니다.
근의 공식이란?
우선, 근의 공식이 무엇인지 간단히 살펴볼까요? 이차방정식의 일반적인 형태는 다음과 같습니다:
ax2 + bx + c = 0
여기서 a , b , c 는 각각 상수(계수)이고, x 는 우리가 찾고자 하는 값, 즉 방정식의 해입니다.
근의 공식은 이 방정식의 해를 구하는데 사용됩니다. 공식은 다음과 같습니다:
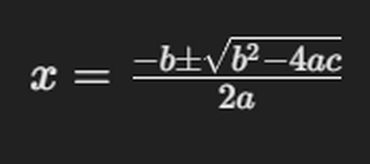
이 공식은 방정식의 해를 구하는 데 아주 유용한 도구입니다.
예를 들어, a = 1 , b = -3 , c = 2 라고 해볼까요?
이때, ax2 + bx + c = 0 이라는 방정식을 풀려면 근의 공식을 이용하면 됩니다.
예시와 함께 알아보는 근의 공식 풀이
문제 예시: x2 – 3x + 2 = 0 을 근의 공식을 사용해 풀어보세요.
계수 a, b, c 값 파악하기:
근의 공식에 대입하기:
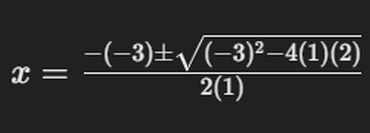
판별식(디스크리민트) 계산하기:
판별식 = (-3)2 – 4(1)(2) = 9 – 8 = 1
근 계산하기:
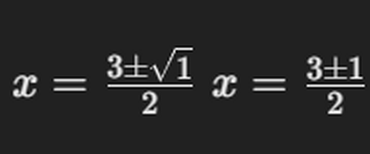
이제 두 개의 해가 나오죠:
즉, x₁ = 2 와
x₂ = 1 이
이 방정식의 해가 됩니다!
마무리하며
이차방정식 풀이가 어렵게 느껴질 때, 이 근의 공식 계산기 를 사용하면 정말 손쉽게 문제를 풀 수 있습니다. 수학이 어렵게 느껴지더라도, 이런 도구를 활용하면 문제를 더 재미있게 해결할 수 있을 거예요. 직접 사용해보시고, 친구들에게도 공유해보세요!
이 글을 통해 여러분이 근의 공식과 이차방정식 풀이에 대해 더 잘 이해하고, 실제로 적용하는 데 도움이 되길 바라요. 계산기를 직접 사용해보면서 수학 문제를 재미있게 풀어보세요!
